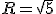Connaissant l'équation d'un cercle trouver son centre et son rayon
Comment à partir d'une équation reconnaître qu'il s'agit d'une équation de cercle et trouver le centre 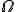 et le rayon R du cercle ?
et le rayon R du cercle ?
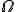 et le rayon R du cercle ?
et le rayon R du cercle ?
On cherche l'ensemble des points M du plan dont les coordonnées x et y vérifient :
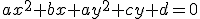 avec
avec
Le coefficient devant les termes en 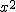 et en
et en 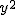 étant le même et non nul, cette équation est une "équation de cercle".
étant le même et non nul, cette équation est une "équation de cercle".
On peut mettre  en facteur et simplifier par
en facteur et simplifier par  ce qui nous donne :
ce qui nous donne :
Ecrivons comme le début d'un carré l'expression :
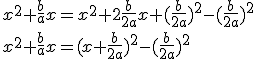 |
Ecrivons comme le début d'un carré l'expression :
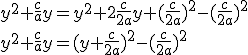 |
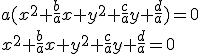
On remplace dans l'équation (1)
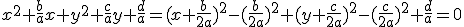
On obtient une équation
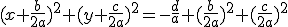
|
|
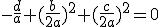 |
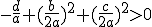 |
| l'ensemble des points M est l'ensemble vide |
l'ensemble des points M est
réduit au point
|
l'ensemble des points M est le cercle
de centre
de rayon
|
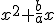
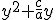
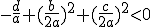
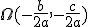
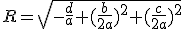
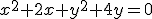 peut s"écrire
peut s"écrire
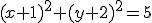
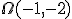 et de rayon
et de rayon